Advent of Code 2025 Day 3 – Lobby

Day 3: Lobby

This year I’m trying to do my Advent of Code solutions in Rust! I started using Rust for work recently, and I’m really enjoying it so far. It’s slightly more complex than Go, but I think it’s worth it for macros especially. Also, this year will only be 12 days instead of 25, which you can read more about here.

Today’s puzzle seems easy at a glance, but I think there’s lots of interesting ways to solve it once you think about a solution.

Part 1

The input for today’s puzzle is a set of lines, with each line consisting of digits from 1-9. For each line, we need to pick the two digits that create the largest number when concatenated. We cannot use the same digit twice, and we need to consider the order of the digits.

For example:

• For the line 987654321111111, the largest number we can create is 98, by concatenating 9 and 8.
• 811111111111119’s largest number is 89.

Then, we need to sum all of these largest numbers from each line to get the final answer.

My Solution

I’ll focus on finding the largest two-digit number from a single line, as that’s the core logic. I had two approaches in mind: one using a stack to keep track of the highest digits encountered, and another using a sliding window to evaluate pairs of digits at a time.

I figured out the sliding window approach first as it’s simpler to implement.

fn get_largest_combo(bank: &[u8]) -> u8 {
    let mut largest_pick: [u8; 2] = [0; 2];

    largest_pick.copy_from_slice(&bank[0..2]);

    for i in 1..=bank.len() - 2 {
        let a = largest_pick[0];
        let b = largest_pick[1];
        let c = bank[i];
        let d = bank[i + 1];

        let picks = [
            ((10 * a) + b, [a, b]),
            ((10 * a) + c, [a, c]),
            ((10 * a) + d, [a, d]),
            ((10 * b) + d, [b, d]),
            ((10 * c) + d, [c, d]),
        ];

        let (_, max_pick) = picks.iter().max_by_key(|(value, _)| *value).unwrap();
        largest_pick = *max_pick;
    }

    (10 * largest_pick[0]) + largest_pick[1]
}

largest_pick keeps track of the two digits that form the largest number found so far. I initialize it with the first two digits of the line, as they are the only option at that point.

While iterating through the line with a sliding window of size 2, I consider the valid combinations that could be formed with the current window’s digits and the digits in largest_pick.

If largest_pick is [a, b] and the current window is [c, d], the valid combinations are:

• ab (the existing largest number)
• ac (replacing b with c from the current window)
• ad (replacing b with d from the current window)
• bd (replacing a with b and using d from the current window)
• cd (using both digits from the current window)

I don’t use bc here, as I use a sliding window and c would have already been considered in a previous iteration. Then, I find the maximum among these combinations and update largest_pick accordingly.

By the end of the iteration, largest_pick contains the two digits that form the largest number possible from the line. I then return this number.

Now to actually solve the puzzle, I call this function for each line in the input and sum the results.

struct Day03 {
    banks: Vec<Vec<u8>>,
}

pub fn part_one(input: &str) -> Option<u64> {
    let day = match Day03::from_str(input) {
        Ok(day) => day,
        Err(error) => {
            eprintln!("Error parsing input: {}", error);
            return None;
        }
    };

    day.banks
        .iter()
        .map(|bank| get_largest_combo(bank))
        .sum::<u64>()
        .into()
}

As always, I’ve only included the relevant parts of the code here, but to see my full solution, you can check out my Advent of Code GitHub repository.

Part 2

The second part of the puzzle builds on the first. This time, instead of just finding the largest two-digit number from each line, we need to find the largest 12-digit number that can be formed by concatenating digits from the line. The same rules apply: we cannot use the same digit twice, and the order of the digits matters.

So for example:

• For 987654321111111, the largest 12-digit number we can form is 987654321111.
• 811111111111119’s largest 12-digit number is 811111111119.

My Solution

Technically, I could have used a sliding window approach again, but the amount of cases to take care of would be huge. Instead I decided to implement a stack-based approach that I had thought of earlier.

fn get_largest_combo_k(bank: &[u8], k: usize) -> u64 {
    let mut stack: Vec<(u8, usize)> = Vec::with_capacity(k); // (digit, original_index)
    let n = bank.len();

    for (i, &digit) in bank.iter().enumerate() {
        // Remove smaller digits from stack if we have room to pick more digits
        while !stack.is_empty() && stack.last().unwrap().0 < digit && stack.len() + (n - i) > k {
            stack.pop();
        }

        if stack.len() < k {
            stack.push((digit, i));
        }
    }

    stack
        .into_iter()
        .map(|(digit, _)| digit)
        .fold(0, |acc, d| acc * 10 + d as u64)
}

This function keeps a stack of k elements, where each element is a tuple containing the digit and its original index in the line. As we iterate through the digits in the line, we check:

• If the stack is not empty,
• If the current digit is larger than the last digit in the stack, and
• If we have enough remaining digits left in the line to still fill the stack to size k.

Once all these conditions are met, we pop the last digit from the stack to make room for the larger current digit, and push the current digit. This ensures that the stack always contains the largest possible digits encountered so far.

After processing all digits, we convert the stack into a single number by concatenating the digits with a fold.

Since this function also works for k = 2, I can reuse it for part 1 as well.

pub fn part_one(input: &str) -> Option<u64> {
    let day = match Day03::from_str(input) {
        Ok(day) => day,
        Err(error) => {
            eprintln!("Error parsing input: {}", error);
            return None;
        }
    };

    day.banks
        .iter()
        .map(|bank| get_largest_combo_k(bank, 2))
        .sum::<u64>()
        .into()
}

pub fn part_two(input: &str) -> Option<u64> {
    let day = match Day03::from_str(input) {
        Ok(day) => day,
        Err(error) => {
            eprintln!("Error parsing input: {}", error);
            return None;
        }
    };

    day.banks
        .iter()
        .map(|bank| get_largest_combo_k(bank, 12))
        .sum::<u64>()
        .into()
}

This actually results in a faster solve time for my part 1 solution as well!

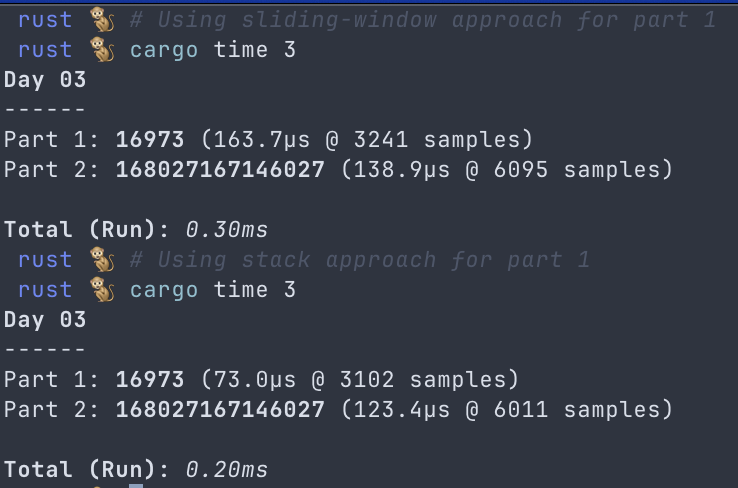
Again, I’ve only included the relevant parts of the code here, check out my repository for the full solution.

That’s it for day 3 of Advent of Code 2025! I hope you enjoyed reading my solution and let’s see how the rest of the month goes!

Vinesh Benny

A Software Engineer learning about different things in life and otherwise

Tweet Share